Getting started

anaStruct is a Python implementation of the 2D Finite Element method for structures. It allows you to do structural analysis of frames and frames. It helps you to compute the forces and displacements in the structural elements.

Besides linear calculations, there is also support for non-linear nodes and geometric non linearity.

Structure object

You start a model by instantiating a SystemElements object. All the models state, i.e. elements, materials and forces are kept by this object.

class anastruct.fem.system.SystemElements(figsize=(12, 8), EA=15000.0, EI=5000.0, load_factor=1.0, mesh=50)

Modelling any structure starts with an object of this class.

Variables

• EA – Standard axial stiffness of elements, default=15,000

• EI – Standard bending stiffness of elements, default=5,000

• figsize – (tpl) Matplotlibs standard figure size

• element_map – (dict) Keys are the element ids, values are the element objects

• node_map – (dict) Keys are the node ids, values are the node objects.

• node_element_map – (dict) maps node ids to element objects.

• loads_point – (dict) Maps node ids to point loads.

• loads_q – (dict) Maps element ids to q-loads.

• loads_moment – (dict) Maps node ids to moment loads.

• loads_dead_load – (set) Element ids that have a dead load applied.

__init__(figsize=(12, 8), EA=15000.0, EI=5000.0, load_factor=1.0, mesh=50)

• E = Young’s modulus

• A = Area

• I = Moment of Inertia

Parameters

• figsize (Tuple[float, float]) – Set the standard plotting size.

• EA (float) – Standard E * A. Set the standard values of EA if none provided when generating an element.

• EI (float) – Standard E * I. Set the standard values of EA if none provided when generating an element.

• load_factor (float) – Multiply all loads with this factor.

• mesh (int) – Plotting mesh. Has no influence on the calculation.

Example

from anastruct import SystemElements
ss = SystemElements()

This ss object now has access to several methods which modify the state of the model. We can for instance create a structure.

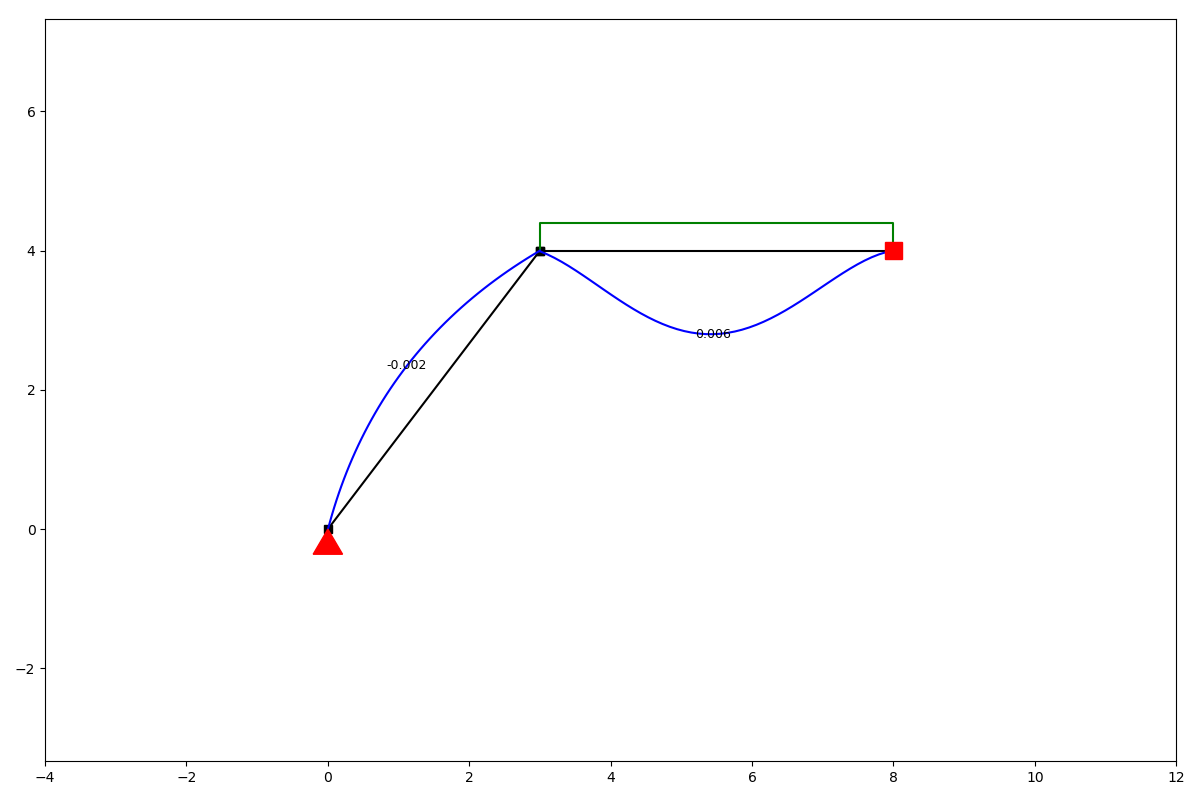
ss.add_element(location=[[0, 0], [3, 4]])
ss.add_element(location=[[3, 4], [8, 4]])

Now we have elements, we need to define the supporting conditions of our structure.

ss.add_support_hinged(node_id=1)
ss.add_support_fixed(node_id=3)

Finally we can add a load on the structure and compute the results.

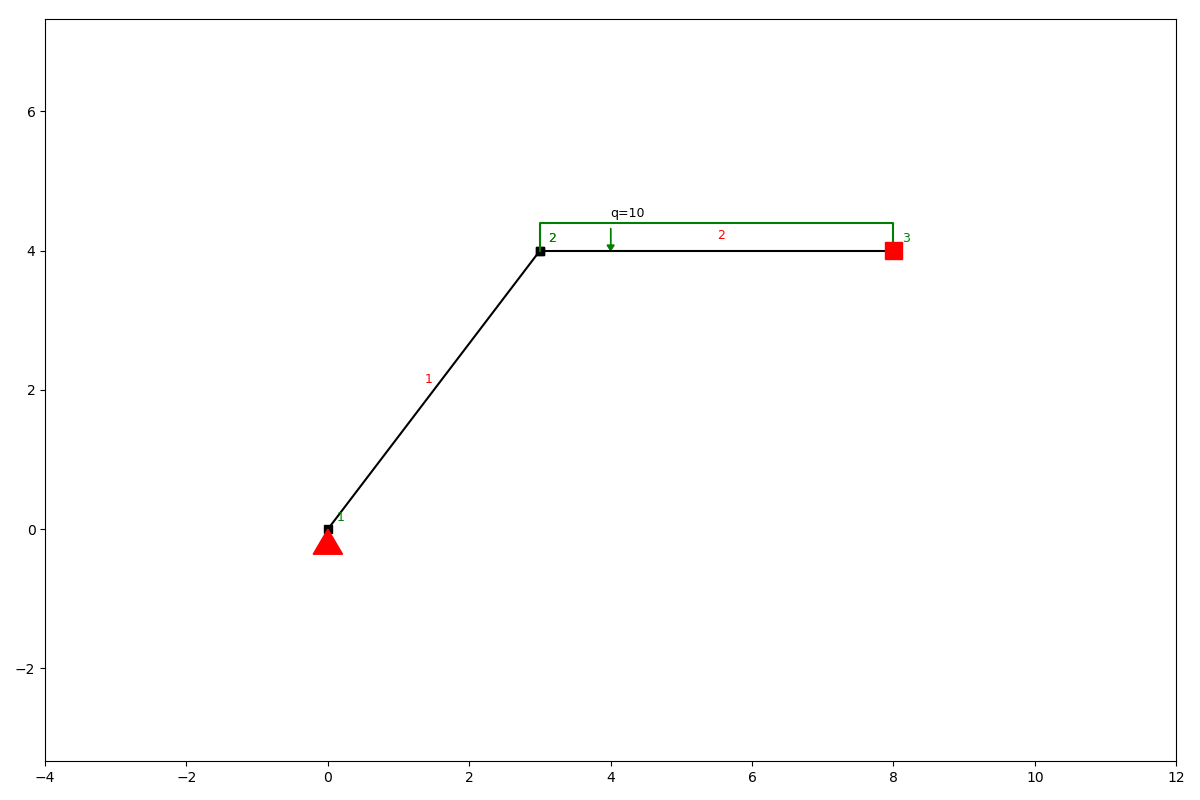
ss.q_load(element_id=2, q=-10)
ss.solve()

We can take a look at the results of the calculation by plotting different units we are interested in.

ss.show_structure()

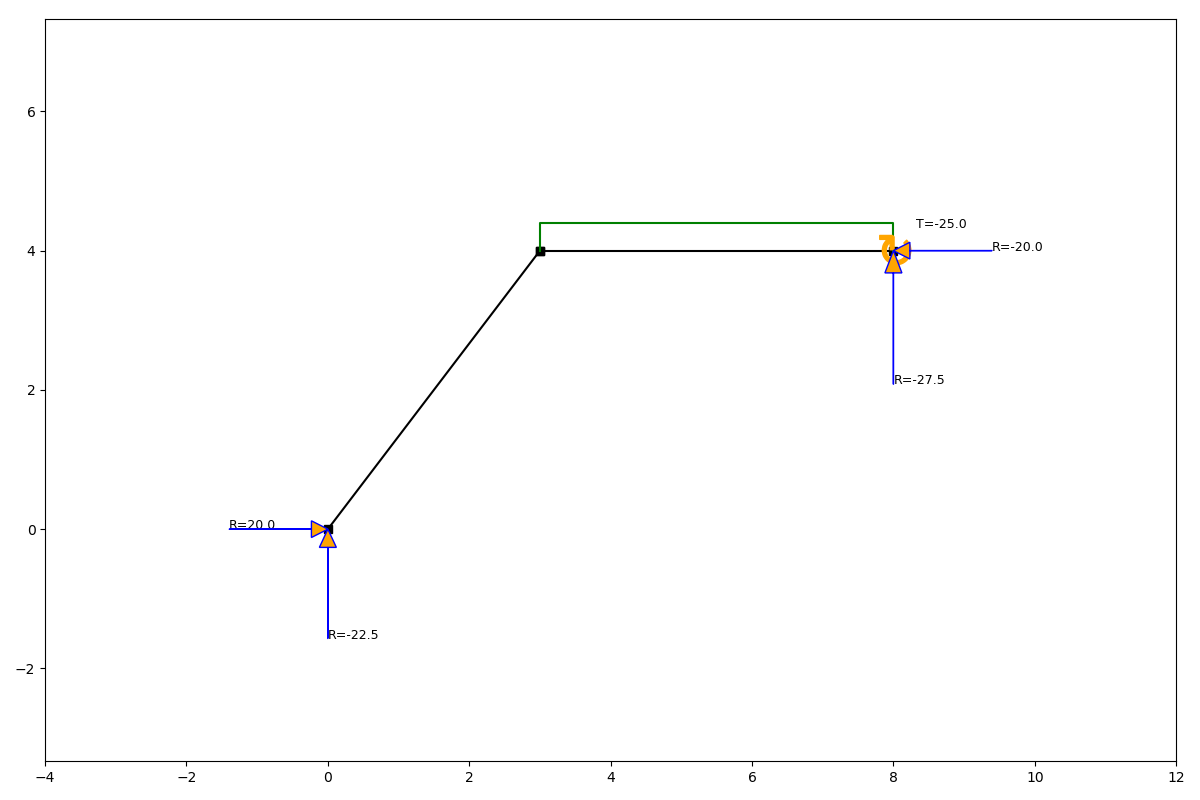
ss.show_reaction_force()

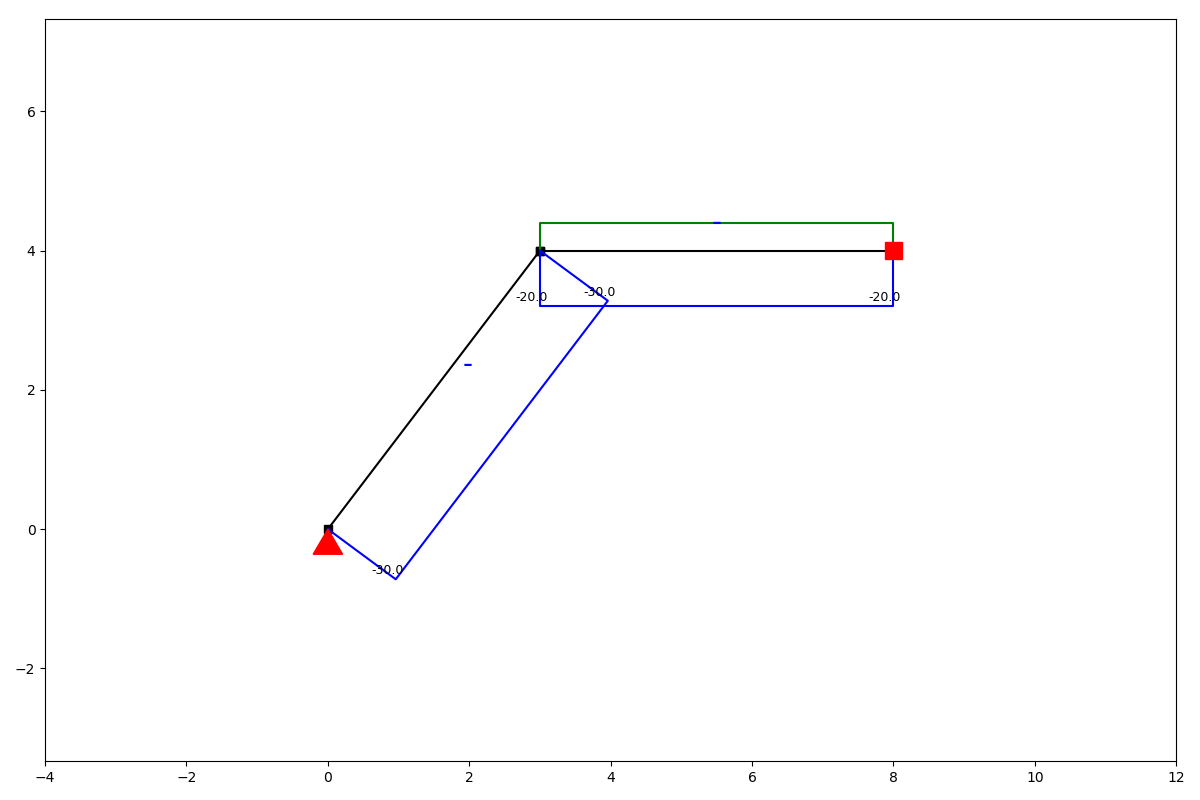
ss.show_axial_force()

ss.show_shear_force()

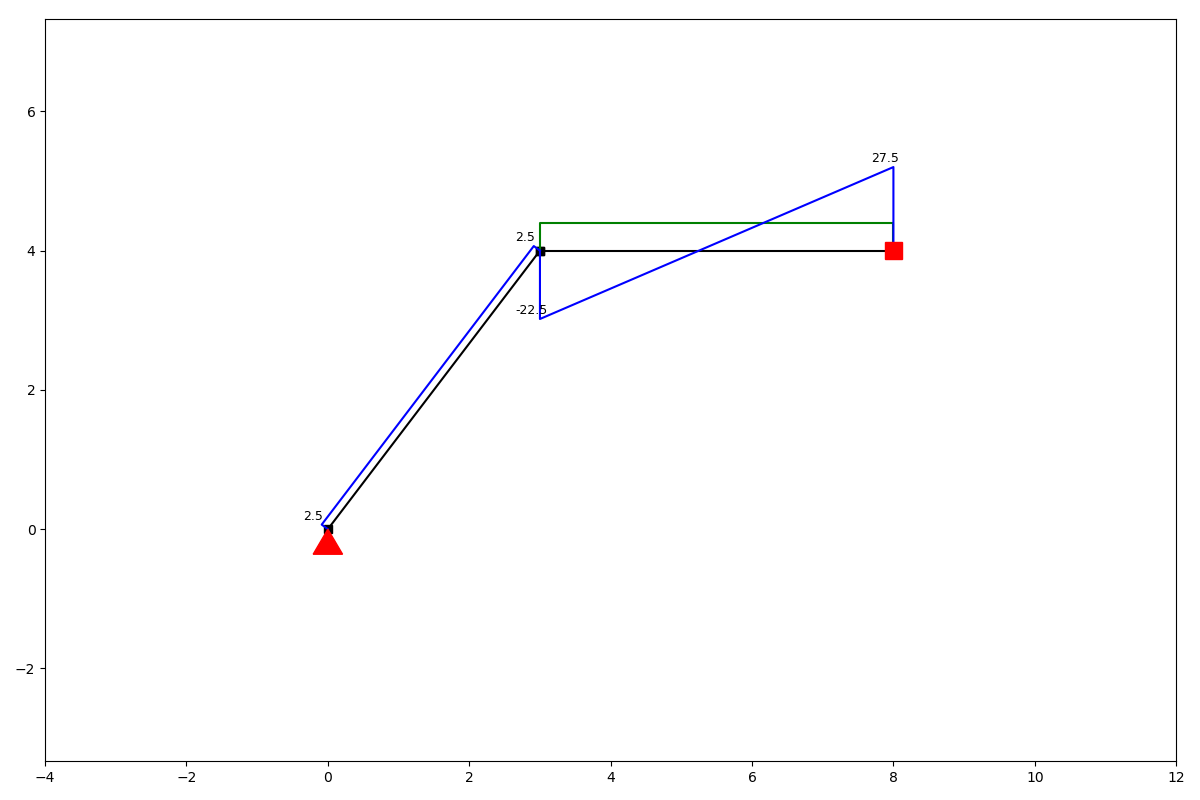
ss.show_bending_moment()

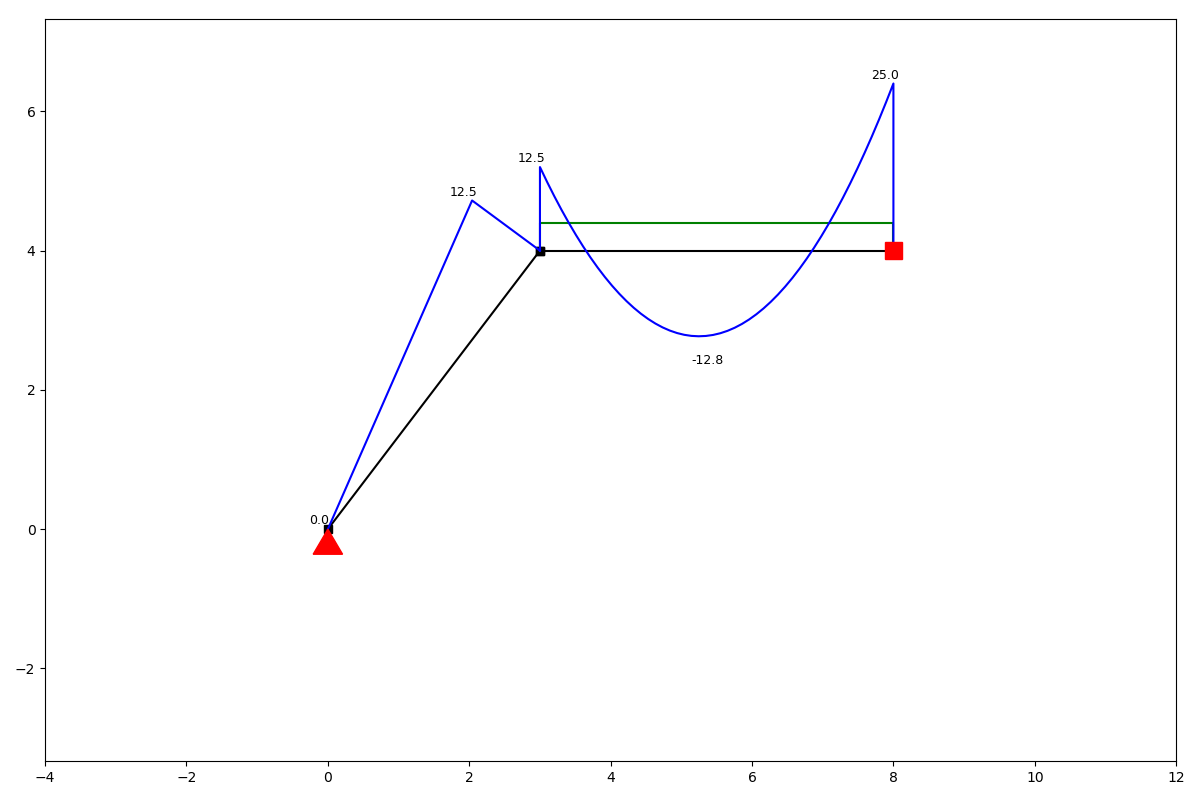
ss.show_displacement()